参考答案：

由A^T=A，得(AP)^T(AP)=P^TA²P，而矩阵．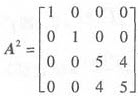

考虑二次型

令y₁=x₁，y₂=x₂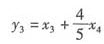，，y₄=x₄，得

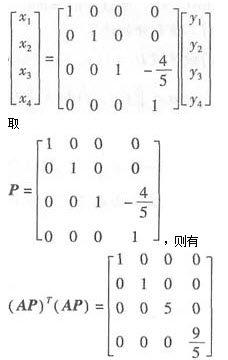
解析：

[考点] 由定义有|3E-A|=0，由此可定出参数y．考虑到A²为对称矩阵，而(AP)^T(AP)=P^TA²P，化其对角矩阵方法有两种：转化为对应二次型x^TA²x，通过非退化线性变换x=Py化为标准形，相应求出P；或者求出A²的特征值、单位化，最后构造出正交矩阵P，本题所求P不唯一