问题
问答题
求函数f(x,y)=x2+xy+y2-3x-6y的极值.
答案
参考答案:
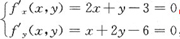 ,得驻点P(0,3).
,得驻点P(0,3).
在P(0,3)点,
A=f"xx(0,3)=2,B=f"xy(0,3)-1,C=f"yy(0,3)=2.
B2-AC=1-4=-3<0,而A=2>0.
从而函数f(x,y)在点P(0,3)有极小值f(0,3)=-9.
解析:
二元函数无条件极值的求解步骤为:(1)先求驻点Mi,即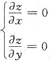 的解(xi,yi);
的解(xi,yi);
(2)求在驻点Mi处的A=f"xx(Mi),B=f"xy(Mi);C=f"yy(Mi),确定B2-AC的符号;
(3)判定:若B2-AC<0,且A<0(A>0),则z=f(xi,yi)为极大(极小)值.

 A="10" V,
A="10" V,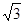 cm,试确定:
cm,试确定: