问题
问答题
设f(x)为连续函数且
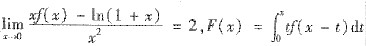，又当x→0时，
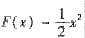与bxk是等价无穷小量，其中常数b≠0，k是正整数．
(Ⅰ)求k与b的值及f(0)．
(Ⅱ)证明f(x)在x=0可导，并求f’(0)．
答案
参考答案：(Ⅰ)[*]
依题意有[*]
由于已知[*]，故[*]，得f(0)=1．
而且[*]
由(*)式得k=3时，
[*]
(Ⅱ)[*]即f(x)在x=0可导，且[*]
解析：[考点] 极限，等价无穷小，变上限定积分，导数综合题