参考答案：C

解析：

即求曲面S：F(x，y，z)=0，其中F(x，y，z)=z+x²+y²-4上点P使S在该点处的法向量n与平面π：2z+2y+z-1=0的法向量n₀=(2，2，1)平行。

S在P(x，y，z)处的法向量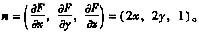n∥n₀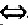n=λn₀，λ为常数，即2x=2λ，2y=2λ，1=λ。即x=1，y=1，又点P(x，y，z)∈S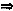z=4-x²-y²_{(x，y)=(1，1)}=2，求得P(1，1，2)(P不在给定的平面上)。