问题
计算题
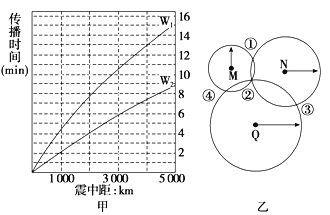
如图所示的直角坐标系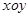
中，在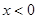
，
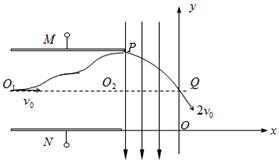
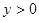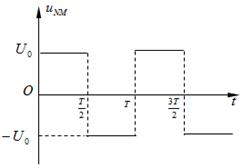
的区域有一对平行金属板M和N，其中N板位于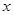
轴上，M、N板加有如图所示电压，平行金属板右侧存在沿y轴负向与平行金属板等宽度的匀强电场，场强大小为E，在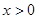
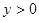的区域存在垂直纸面的矩形有界磁场，其下边界和左边界分别与
、
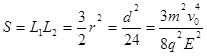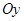轴重合。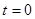
时刻一质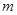量为
，电量为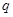
的带电微粒沿着平金属板的轴线
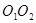以初速度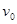
向右开始运动，恰从M板右边缘的P点沿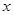轴正向进入平行金属板右侧电场，经过一段时间后以
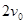的速度经Q点进入磁场，Q点为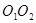与y轴的交点，再经磁场偏转带电微粒恰好从坐标原点
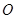沿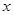轴负向返回电场，不计带电微粒的重力。求：
（1）平行金属板M、N间的距离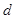
及右侧电场的宽度
；
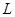（2）平行金属板上所加电压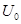
满足的条件；
（3）矩形磁场区域的最小面积。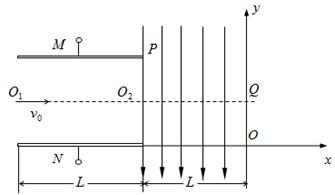
答案
（1）
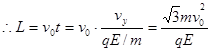（2）
（
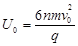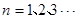）（3）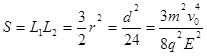
（1）因带电微粒在P点速度沿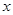
轴正向，则带电微粒在Q点的与水平速度为
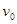，设速度方向夹角为
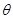，有：
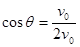
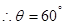（1分）
在Q点的竖直方向分速度为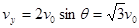
（1分）
从P点到Q点，带电微粒做类平抛运动：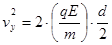
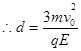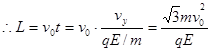（2分）
（2分）
（2）平行金属板间粒子的运动轨迹如图，粒子在电场中运动侧向总位移满足：
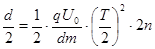（2分） 又
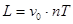其中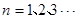（） （2分）
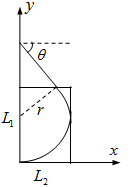
由上面两式可解得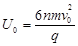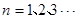： （）（2分）
（3）如图，设最小的矩形磁场的高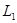为
，宽为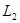
，
画出带电粒子的运动轨迹，则由几何知识可知：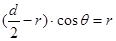
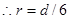
故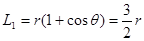
；
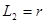。（2分）
可得矩形磁场的最小面积为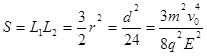：（2分）
