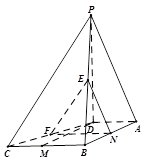
如图,在四棱锥P-ABCD中,PD⊥面ABCD,AD∥BC,CD=13,AB=12,BC=10,AD =12 BC. 点E、F分别是棱PB、边CD的中点.(1)求证:AB⊥面PAD; (2)求证:EF∥面PAD
(1)要证明线面垂直,关键是要通过线线垂直的证明,结合判定定理来得到,关键点 一步是AD⊥AB.
(2)要证明线面平行,关键是要通过线线平行的证明,结合判定定理来得到,通过做适当的辅助线,结合三角形的中位线平移,得到EF∥DQ.
题目分析:证明:(1)因为PD⊥面ABCD,
所以PD⊥AB. 2分
在平面ABCD中,D作DM//AB,则由AB=12得
DM=12.又BC=10,AD=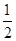 BC,则AD=5,从而CM=5.
BC,则AD=5,从而CM=5.
于是在△CDM中,CD=13,DM=12,CM=5,则
由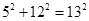 及勾股定理逆定理得DM⊥BC .
及勾股定理逆定理得DM⊥BC .
又DM//AB,BC//AD,所以AD⊥AB.
又PD∩AD=D,所以AB⊥面PAD. 6分
(2)[证法一] 取AB的中点N,连结EN、FN.
因为点E是棱PB的中点,所以在△ABP中,EN//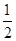 PA.
PA.
又PAÌ面PAD,所以EN//面PAD. 8分
因为点F分别是边CD的中点,所以在梯形ABCD中,FN//AD.
又ADÌ面PAD,所以FN//面PAD. 10分
又EN∩FN=N,PA∩DA=A,所以面EFN//面PAD. 12分
又EFÌ面EFN,则EF//面PAD. 14分
[证法二] 延长CD,BA交于点G.
连接PG,EG,EG与PA交于点Q.
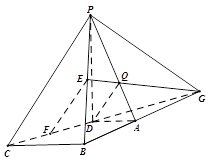
由题设AD∥BC,且AD=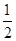 BC,所以CD=DG,BA
BC,所以CD=DG,BA
=AG,即点A为BG的中点.
又因为点E为棱PB的中点,所以EA为△BPG的中位线,即EA∥PG,且EA:PG=1:2,故有EA:PG=EQ:QG=1:2. 10分
又F是边CD的中点,并由CD=DG,则有FD:DG
=1:2. 12分
在△GFE中,由于EQ:QG=1:2,FD:DG=1:2,所以EF∥DQ.
又EFË面PAD,而DQÌ面PAD,所以EF∥面PAD. 14分
点评:解决该试题的关键是熟练的结合线面平行和垂直的判定定理,找到线线的平行和垂直关系,属于基础题。
