问题
解答题
设函数y=f（x）=ax3+bx2+cx+d的图象在x=0处的切线方程为24x+y-12=0，
（Ⅰ）求c，d；
（Ⅱ）若函数在x=2处取得极值-16，试求函数解析式并确定函数的单调区间。
答案
解：（Ⅰ）f（x）的定义域为R，
，
∴
；
∵切线24x+y-12=0的斜率为k=-24，
∴c=-24；
把x=0代入24x+y-12=0得y=12，
∴P（0，12），
∴d=12，
∴c=-24，d=12。
（Ⅱ）由（Ⅰ）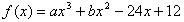
，
由已知得：
，
∴
，
∴
，
∴
，
由
；
由
；
∴f（x）的单调增区间为
；单调减区间为（-4，2）。