解：（1）f'（x）=3ax²+2bx﹣3．

根据题意，得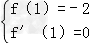 

即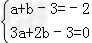 

解得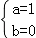 

所以f（x）=x³﹣3x．

（2）令f'（x）=0，即3x²﹣3=0．得x=±1．

当x∈（﹣∞，﹣1）时，f′（x）＞0，函数f（x）在此区间单调递增；

当x∈（﹣1，1）时，f′（x）<0，函数f（x）在此区间单调递减；

因为f（﹣1）=2，f（1）=﹣2，

所以当x∈[﹣2，2]时，f（x）_max=2，f（x）_min=﹣2．

则对于区间[﹣2，2]上任意两个自变量的值x₁，x₂，都有

|f（x₁）﹣f（x₂）|≤|f（x）_max﹣f（x）_min|=4，

所以c≥4．

所以c的最小值为4．

（3）因为点M（2，m）（m≠2）不在曲线y=f（x）上，

所以可设切点为（x₀，y₀）．则

y₀=x₀³﹣3x₀．

因为f'（x₀）=3x₀²﹣3，所以切线的斜率为3x₀²﹣3．

则3x₀²﹣3= ，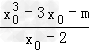

即2x₀³﹣6x₀²+6+m=0．

因为过点M（2，m）（m≠2）可作曲线y=f（x）的三条切线，

所以方程2x₀³﹣6x₀²+6+m=0有三个不同的实数解．

所以函数g（x）=2x³﹣6x²+6+m有三个不同的零点．

则g'（x）=6x²﹣12x．

令g'（x）=0，则x=0或x=2．

当x∈（﹣∞，0）时，g′（x）＞0，函数g（x）在此区间单调递增；

当x∈（0，2）时，g′（x）<0，函数g（x）在此区间单调递增；

所以，函数g（x）在x=0处取极大值，在x=2处取极小值，

有方程与函数的关系知要满足题意必须满足：  ，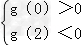

即 ，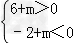

解得﹣6＜m＜2．