问题
解答题
| 函数f(x)=aex,g(x)=lnx-lna,其中a为常数,且函数y=f(x)和y=g(x)的图象在其与坐标轴的交点处的切线互相平行 (1)求函数y=g(x)的解析式; (2)若关于x的不等式
|
答案
(1)∵函数f(x)=aex,g(x)=lnx-lna,
∴f/(x)=aex,g/(x)=1 x
∴y=f(x)的图象与坐标轴的交点为(0,a),
y=g(x)的图象与坐标轴的交点为(a,0)
由题意得f′(0)=g′(a),即a=
,1 a
又∵a>0,
∴a=1,
∴g(x)=lnx
(2)由题意g(x)≠0,
∴x>0,x≠1
当x∈(1,+∞)时,
>x-m lnx
⇔m<x-x
lnxx
令φ(x)=x-
lnx,x
∴φ/(x)=2
-lnx-2x 2 x
令h(x)=2
-lnx-2,x
∴h/(x)=
(1-1 x
)1 x
当x∈(1,+∞)时,h′(x)>0,
∴h(x)单调递增.
∴h(x)>h(1)=0
由m<x-
lnx在x∈(1,+∞)上恒成立,得m≤φ(1)=1x
当x∈(0,1)时,
>x-m lnx
⇔m>x-x
lnxx
可得φ/(x)=
>0,h(x) 2 x
∴φ(x)单调递增.
由m>x-
lnx=φ(x)在x∈(0,1)上恒成立,x
得m≥φ(1)=1,
综上,可知m=1;

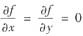 ,则f(x,y)≡常数.
,则f(x,y)≡常数. ,则f(x,y)≡常数.
,则f(x,y)≡常数.