问题
单项选择题
设f(x，y)为区域D内的函数，则下列命题中不正确的是
(A) 若在D内，有
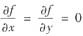，则f(x，y)≡常数．
(B) 若在D内的任何一点处沿两个不共线方向的方向导数都为零，则f(x，y)≡常数．
(C) 若在D内，有df(x，y)≡0，则f(x，y)≡常数．
(D) 若在D内，有
，则f(x，y)≡常数．
答案
参考答案：D
解析： 考生应该掌握这一结论：
在区域D，
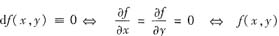为常数．
于是结论(A)、(C)是正确的．
现在如果能在(B)与(D)中证明其中之一是正确的或举例说明其中一个是错误的，则就可作出正确的选择．
方法1° 考察(B)．设(x0，y0)∈D为任意一点，它存在两个不共线的方向：ιi=(cosαi，cosβi)(i=1，2)，使得
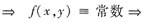(B)正确，因此应选(D)
方法2° 考察(D)．在极坐标变换x=rcosθ，y=rsinθ下，
即
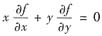，这仅能表示f(x，y)与r无关，不能说明f(x，y)为常数．
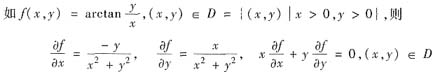
但f(x，y)在D上不恒为常数，因此应选(D)．