搜题请搜索小程序“爱下问搜题”
问题 解答题

设 f（x）=x3-6x+5求函数f（x）的单调区间及其极值．

答案

由 f（x）=x3-6x+5，得：f′(x)=3x2-6=3(x+

2
)(x-
2
)．

由f′(x)=3(x+

2
)(x-
2
)=0，得：x=-
2
或x=
2
．

列表：

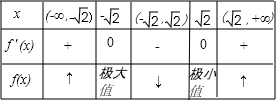
由表可知，函数的增区间为(-∞，-

2
)，(
2
，+∞)，减区间为(-
2
，
2
)．

当x=-

2
时函数取得极大值f(-
2
)=(-
2
)3-6×(-
2
)+5=5+4
2
；当x=
2
时函数取得极小值f(
2
)=(
2
)3-6
2
+5=5-4
2
．

判断题

特种设备使用单位未依照《特种设备安全监察条例》第二十七条的规定，对在用特种设备进行经常性日常维护保养和定期自行检查的，或者对在用特种设备的安全附件、安全保护装置、测量调控装置及有关附属仪器仪表进行定期校验、检修，并作出记录的，由特种设备安全监督管理部门责令限期改正；逾期未改正的，处1万元以上5万元以下罚款；情节严重的，责令停止使用或者停产停业整顿。
查看答案
单项选择题

有关药品包装、标签和说明书的说法，错误的是（）

A.药品包装必须按照规定印有或者贴有标签

B.药品说明书和标签由省级药品监督管理部门予以核准

C.药品说明书和标签中的文字应当清晰易辨，标识应当清楚醒目

D.药品生产企业生产供上市销售的最小包装必须附有说明书
查看答案