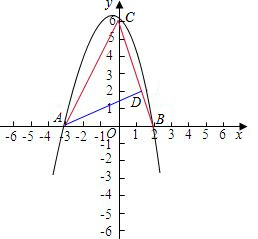∵二次函数y=-x²+（m-2）x+3（m+1）的图象与x轴交于A、B两点（A在B左边），

∴设A、B的坐标为（x₁，0），（x₂，0），

∴OA=|x₁|，OB=|x₂|，

∴x₁+x₂=-（m-2），x₁x₂=-3（m+1），

而线段AO与OB的长的积等于6，

∴3（m+1）=±6，

∴m=1或-3，

当m=1时，抛物线解析式为y=-x²-x+6，

∴A、B的坐标为（-3，0），（2，0），C（0，6）

∴AC=3

5

，BC=2

10

，AB=5，

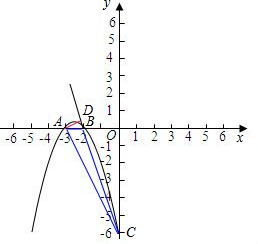
如图抛物线过A作AD⊥BC于D，

则S_△ABC=

1

2

CO•BA=

1

2

AD•BC，

∴AD=

CO×BA

BC

=

3

4

10

，

∴sinC=

AD

AC

=

2

4

；

当m=-3时，抛物线解析式为y=-x²-5x-6，

∴A、B的坐标为（-3，0），（-2，0），C（0，-6）

∴AC=3

5

，BC=2

10

，AB=1，

如图抛物线过A作AD⊥BC于D，

则S_△ABC=

1

2

CO•BA=

1

2

AD•BC，

∴AD=

CO×BA

BC

=

3

10

10

，

∴sinC=

AD

AC

=

2

10

；

所以sinC的值为

2

4

或

2

10

．