问题
填空题
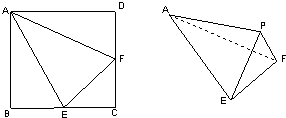
已知正方形ABCD的边长为2,E,F分别为BC,DC的中点,沿AE,EF,AF折成一个四面体,使B,C,D三点重合,则这个四面体的体积为______.
答案
以AE,EF,AF为折痕,折叠这个正方形,使点B,C,D重合于一点P,得到一个四面体,如图所示.
∵在折叠过程中,
始终有AB⊥BE,AD⊥DF,
即AP⊥PE,AP⊥PF,
所以AP⊥平面EFP.
四面体的底面积为:S△EFP=
PE•PF,高为AP=21 2
∴四面体A-EFP的体积:V A-EFP=
×1 3
×1×1×2=1 2
.1 3
故答案为:
.1 3