已知函数f(x)=
(Ⅰ)当m>0时,求函数的单调区间; (Ⅱ)当m≥1时,曲线C:y=f(x)在点P(0,1)处的切线l与C有且只有一个公共点,求m的取值的集合M. |
由题设知:f′(x)=mx-2+
(x>-1)1 x+1
(Ⅰ)当m>0时,f′(x)=
=mx2-(m-2)x-1 x+1
(x-m x+1
)(x-2-m- m2+4 2m
),
-m+2m2+4 2m
而
>0>
-m+2m2+4 2m
;2-m- m2+4 2m
-(-1)=2-m- m2+4 2m
>0m+2- m2+4 2m
∴函数f(x)单调递增区间为(-1,-
)∪(m-2+ m2+4 2m
,+∞);
-m+2m2+4 2m
单调递减区间为(-
,m-2+ m2+4 2m
).
-m+2m2+4 2m
(Ⅱ)由题设知:P∈C,f'(0)=-1,切线l的方程为y=-x+1,
于是方程:-x+1=
mx2-2x+1+ln(x+1),即1 2
mx2-x+ln(x+1)=0有且只有一个实数根;1 2
设g(x)=
mx2-x+ln(x+1),得g(0)=0;1 2
g′(x)=
=mx2+(m-1)x x+1
[x-(mx x+1
-1)],1 m
当m=1时,g′(x)=
≥0,g(x)为增函数,符合题设;x2 x+1
当m>1时,有-1<
-1<0,得x∈(0,+∞),1 m
g'(x)>0,g(x)在此区间单调递增,g(x)>0;
x∈(
-1,0),g′(x)<0,g(x)在此区间单调递减,g(x)>0;1 m
x∈(-1,
-1),g′(x)>0,g(x)在此区间单调递增,g(x)∈(-∞,g(1 m
-1));1 m
此区间存在零点,即得m>1不符合题设;
∴由上述知:M={1}.

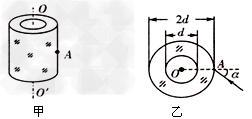
 ,图乙是它的截面.有一束光线从玻璃管的外侧面上的A点垂直于玻璃管中心轴线射入.若入射角α为60°,则有无光线从玻璃管的外壁射出玻璃管?如果有,则有光线射出的位置有几处,并求出各处射出的光线与A点入射光线的夹角是多大?如果没有,请说明理由.需作出光路图。
,图乙是它的截面.有一束光线从玻璃管的外侧面上的A点垂直于玻璃管中心轴线射入.若入射角α为60°,则有无光线从玻璃管的外壁射出玻璃管?如果有,则有光线射出的位置有几处,并求出各处射出的光线与A点入射光线的夹角是多大?如果没有,请说明理由.需作出光路图。