问题
解答题
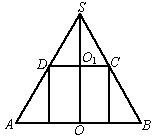
圆锥的底面半径为5 cm，高为12 cm，当它的内接圆柱的底面半径为何值时，圆锥的内接圆柱全面积有最大值？最大值是多少?
答案
2π（12x－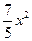
） 
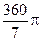cm2
如图SAB是圆锥的轴截面，其中SO＝12，OB＝5．设圆锥内接圆柱底面半径为O1C＝x，由△SO1C∽△SOB，
则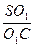
＝
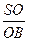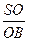，SO1＝·O1C＝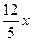
，
∴OO1＝SO－SO1＝12－，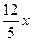
则圆柱的全面积S＝S侧＋2S底＝2π（12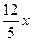－）x＋2πx2＝2π（12x－）．
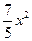当x＝
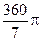cm时，S取到最大值cm2．
