问题
解答题
定义:两个连续函数(图象不间断)f(x),g(x)在区间[a,b]上都有意义,我们称函数|f(x)+g(x)|在[a,b]上的最大值叫做函数f(x)与g(x)在区间[a,b]上的“绝对和”.
(1)试求函数f(x)=x2与g(x)=x(x+2)(x-4)在闭区间[-2,2]上的“绝对和”.
(2)设hm(x)=-4x+m及f(x)=x2都是定义在闭区间[1,3]上,记hm(x)与f(x)的“绝对和”为Dm,如果D(m)的最小值是D(m0),则称f(x)可用hm0(x)“替代”,试求m0的值,使f(x)可用hm0(x)“替代”.
答案
(1)令F(x)=f(x)+g(x)=x2+x(x+2)(x-4)=x3-x2-8x,
则F'(x)=3x2-2x-8=(3x+4)(x-2).F(x),F'(x)随x的值的变化情况如下表
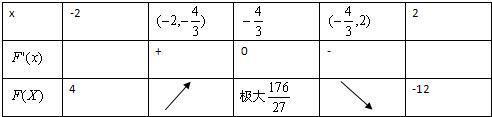
由表可知F(x)的值域为[-12,
].176 27
故|f(x)+f(x)|在[-2,2]上的最大值为12.
从而f(x)与g(x)在[-2,2]上的“绝对和”为12.
(2)设ϕ(x)=hm(x)+f(x)=-4x+m+x2=(x-2)2+m-4.
而ϕ(1)=ϕ(3)=m-3∴D(m)是|m-3|与|m-4|中较大者.
∴D(m)=|m-4|(m<
)7 2 |m-3|(m≥
)7 2
∴当m=
时,D(m)最小,∴m0=7 2
.7 2
即m0=
时,f(x)可用hm0(x)“替代”7 2
