问题
解答题
函数y=ax2(a≠0)与直线y= 2x﹣3交于(1,b),求:
(1)a和b的值;
(2)求抛物线y= ax2的解析式,并求顶点坐标和对称轴;
(3)x取何值时,二次函数y= ax2中的y随x的增大而增大;
(4)求抛物线与直线y= ﹣2的两交点及顶点所构成的三角形面积.
答案
解:(1)将x=1,y=b代入y=2x-3中,得b=﹣1,
∴交点坐标是(1,﹣1).
再将x=1,y= ﹣1代入y=ax2中,解得a=﹣1,
∴a=﹣1,b=﹣1;
(2)抛物线的解析式为y= ﹣x2,顶点坐标为(0,0),
对称轴为直线x=0(即y轴);
(3)当x<0时,y随x的增大而增大;
(4)设直线y=﹣2与y= ﹣x2相交于A、B两点(如答图1),
由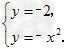
解得A(﹣ ,﹣2),B(
,﹣2),B( ,﹣2),
,﹣2),
∴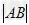 =
= ﹣(﹣
﹣(﹣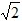 )=
)=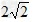 ,
, =2,
=2,
∴S△AOB= ×
×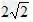 ×2.
×2.
单项选择题
计算题

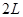 的AB、CD两直线间的区域存在着两个大小不同、方向相反的有界匀强电场,其中PT上方的电场
的AB、CD两直线间的区域存在着两个大小不同、方向相反的有界匀强电场,其中PT上方的电场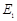 的场强方向竖直向下,PT下方的电场
的场强方向竖直向下,PT下方的电场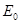 的场强方向竖直向上,在电场左边界AB上宽为
的场强方向竖直向上,在电场左边界AB上宽为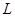 的PQ区域内,连续分布着电量为
的PQ区域内,连续分布着电量为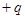 、质量为
、质量为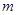 的粒子。从某时刻起由Q到P点间的带电粒子,依次以相同的初速度
的粒子。从某时刻起由Q到P点间的带电粒子,依次以相同的初速度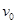 沿水平方向垂直射入匀强电场
沿水平方向垂直射入匀强电场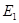 后从CD边上的M点水平射出,其轨迹如图,若MT两点的距离为
后从CD边上的M点水平射出,其轨迹如图,若MT两点的距离为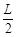 。不计粒子的重力及它们间的相互作用。试求:
。不计粒子的重力及它们间的相互作用。试求: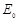 与
与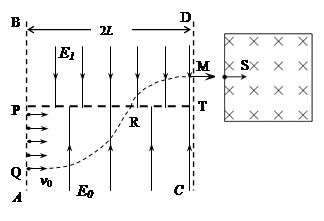 (3)有一边长为
(3)有一边长为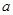 、由光滑绝缘壁围成的正方形容器,在其边界正中央开有一小孔S,将其置于CD右侧,若从Q点射入的粒子经AB、CD间的电场从S孔水平射入容器中。欲使粒子在容器中与器壁多次垂直碰撞后仍能从S孔射出(粒子与绝缘壁碰撞时无能量和电量损失),并返回Q点,在容器中现加上一个如图所示的匀强磁场,粒子运动的半径小于
、由光滑绝缘壁围成的正方形容器,在其边界正中央开有一小孔S,将其置于CD右侧,若从Q点射入的粒子经AB、CD间的电场从S孔水平射入容器中。欲使粒子在容器中与器壁多次垂直碰撞后仍能从S孔射出(粒子与绝缘壁碰撞时无能量和电量损失),并返回Q点,在容器中现加上一个如图所示的匀强磁场,粒子运动的半径小于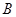 的大小还应满足什么条件?
的大小还应满足什么条件?