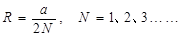(16分)如图所示,相距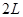 的AB、CD两直线间的区域存在着两个大小不同、方向相反的有界匀强电场,其中PT上方的电场
的AB、CD两直线间的区域存在着两个大小不同、方向相反的有界匀强电场,其中PT上方的电场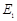 的场强方向竖直向下,PT下方的电场
的场强方向竖直向下,PT下方的电场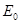 的场强方向竖直向上,在电场左边界AB上宽为
的场强方向竖直向上,在电场左边界AB上宽为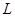 的PQ区域内,连续分布着电量为
的PQ区域内,连续分布着电量为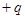 、质量为
、质量为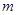 的粒子。从某时刻起由Q到P点间的带电粒子,依次以相同的初速度
的粒子。从某时刻起由Q到P点间的带电粒子,依次以相同的初速度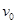 沿水平方向垂直射入匀强电场
沿水平方向垂直射入匀强电场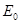 中,若从Q点射入的粒子,通过PT上的某点R进入匀强电场
中,若从Q点射入的粒子,通过PT上的某点R进入匀强电场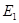 后从CD边上的M点水平射出,其轨迹如图,若MT两点的距离为
后从CD边上的M点水平射出,其轨迹如图,若MT两点的距离为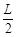 。不计粒子的重力及它们间的相互作用。试求:
。不计粒子的重力及它们间的相互作用。试求:
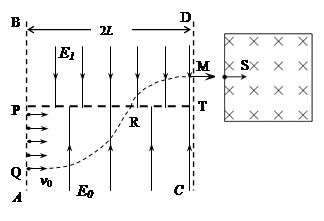
(1)电场强度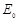 与
与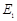 ;
;
(2)在PQ间还有许多水平射入电场的粒子通过电场后也能垂直CD边水平射出,这些入射点到P点的距离有什么规律?
 (3)有一边长为
(3)有一边长为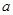 、由光滑绝缘壁围成的正方形容器,在其边界正中央开有一小孔S,将其置于CD右侧,若从Q点射入的粒子经AB、CD间的电场从S孔水平射入容器中。欲使粒子在容器中与器壁多次垂直碰撞后仍能从S孔射出(粒子与绝缘壁碰撞时无能量和电量损失),并返回Q点,在容器中现加上一个如图所示的匀强磁场,粒子运动的半径小于
、由光滑绝缘壁围成的正方形容器,在其边界正中央开有一小孔S,将其置于CD右侧,若从Q点射入的粒子经AB、CD间的电场从S孔水平射入容器中。欲使粒子在容器中与器壁多次垂直碰撞后仍能从S孔射出(粒子与绝缘壁碰撞时无能量和电量损失),并返回Q点,在容器中现加上一个如图所示的匀强磁场,粒子运动的半径小于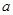 ,磁感应强度
,磁感应强度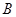 的大小还应满足什么条件?
的大小还应满足什么条件?
(1)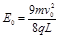 、
、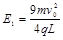
(2)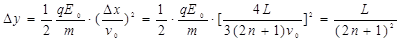 (n=0、1、2、3、……)
(n=0、1、2、3、……)
(3)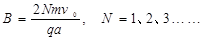 或
或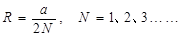
(解法一)(1)设粒子经PT直线上的点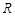 由
由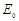 电场进入
电场进入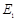 电场,由Q到
电场,由Q到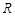 及
及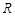 到
到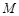 点的时间分别为
点的时间分别为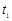 与
与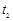 ,到达
,到达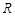 时竖直速度为
时竖直速度为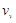 ,由运动学公式可知:
,由运动学公式可知:
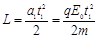 …………①
…………①
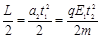 …………②
…………②
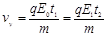 …………③
…………③
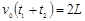 …………④
…………④
由①②③④式解得: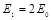 ,
,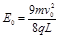 、
、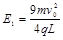 。
。
(解法二)(1)由图知粒子从两板间射出箭后速度方向未发生变化得上下两磁场对粒子做功相等,即: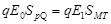 ,又∵
,又∵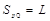 ,
,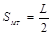
∴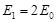 …………①
…………①
粒子从Q运动到M点总时间为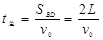
在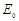 电场运动的时间
电场运动的时间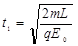
在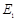 电场运动的时间:
电场运动的时间: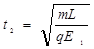
∴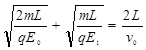 …………②
…………②
由①②式解得: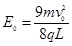 ,
,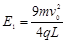
(2)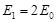 及③式可得:
及③式可得: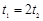 ,因沿PT方向粒子做匀速运动,故P、R两点间的距离是R、T两点间距离的两倍。即粒子在
,因沿PT方向粒子做匀速运动,故P、R两点间的距离是R、T两点间距离的两倍。即粒子在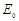 电场做类平抛运动在PT方向的位移是在
电场做类平抛运动在PT方向的位移是在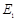 电场中的两倍。
电场中的两倍。
设PQ间到P点距离为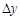 的F处射出的粒子通过电场后也沿水平方向,若粒子第一次达PT直线用时
的F处射出的粒子通过电场后也沿水平方向,若粒子第一次达PT直线用时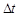 ,水平位移为
,水平位移为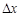 ,则:
,则: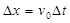 、
、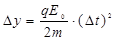
粒子在电场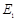 中可能做类平抛运动后垂直CD边射出电场,也可能做类斜抛运动后返回
中可能做类平抛运动后垂直CD边射出电场,也可能做类斜抛运动后返回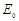 电场,在
电场,在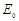 电场中做类平抛运动垂直CD水平射出,或在
电场中做类平抛运动垂直CD水平射出,或在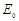 电场中做类斜抛运动再返回
电场中做类斜抛运动再返回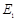 电场。
电场。
若粒子从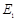 电场垂直CD射出电场,则:
电场垂直CD射出电场,则: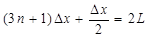 ,(n=0、1、2、3、……)
,(n=0、1、2、3、……)
解得: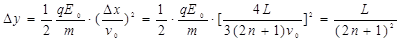 (n=0、1、2、3、……)
(n=0、1、2、3、……)
若粒子从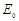 电场垂直CD射出电场,则
电场垂直CD射出电场,则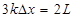 (k=1、2、3、……)
(k=1、2、3、……)
解得: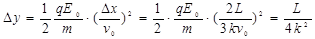 (k=1、2、3、……)
(k=1、2、3、……)
即PF间的距离为: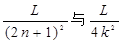 其中n=0、1、2、3、……,k=1、2、3、……
其中n=0、1、2、3、……,k=1、2、3、……
或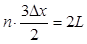 (n=1、2、3、……
(n=1、2、3、……
解得: (n=1、2、3、……)
(n=1、2、3、……)
即PF间的距离为: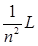 (n=1,2,3,……)
(n=1,2,3,……)
 (3)(6分)欲使粒子仍能从S孔处射出,粒子的运动轨迹可能是如图甲、乙所示的两种情况。对图甲所示的情形,粒子运动的半径为
(3)(6分)欲使粒子仍能从S孔处射出,粒子的运动轨迹可能是如图甲、乙所示的两种情况。对图甲所示的情形,粒子运动的半径为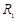 ,则
,则
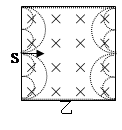
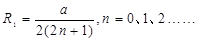
又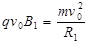
解得: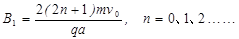
对图乙所示的情形,粒子运动的半径为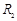 ,
,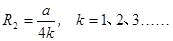
又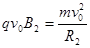
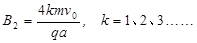
综合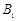 、
、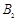 得:
得: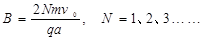
或