问题
解答题
已知函数f(x)=x2+bx+c(b，c∈R)，对任意的x∈R，恒有f′(x)≤f(x)，
(Ⅰ)证明：当x≥0时，f(x)≤(x+c)2；
(Ⅱ)若对满足题设条件的任意b，c，不等式f(c)-f(b)≤M(c2-b2)恒成立，求M的最小值．
答案
解：(Ⅰ)易知f′(x)=2x+b，由题设，对任意的x∈R，2x+b≤x2+bx+c，
即x2+(b-2)x+c-b≥0恒成立，
所以(b-2)2-4(c-b)≤0，从而
，
于是c≥1，且
=|b|，
因此2c-b=c+(c-b)＞0，
故当x≥0时，有(x+c)2-f(x)=(2c-b)x+c(c-1)≥0，
即当x≥0时，f(x)≤(x+c)2。
(Ⅱ)由(Ⅰ)知，c≥|b|，
当c＞|b|时，有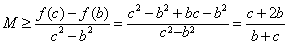
，
令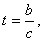
则
，
而函数g(t) =2-
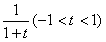的值域是
；
因此，当c＞|b|时，M的取值集合为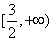
；
当c=|b|时，由(Ⅰ)知，b=±2，c=2，此时f(c)-f(b)=-8或0，
c2-b2=0，从而f(c)-f(b)≤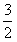
(c2-b2)恒成立；
综上所述，M的最小值为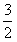。