问题
解答题
已知二次函数y=ax2+bx+c(a≠0)自变量x与函数值y之间满足下列数量关系:
(2)这个二次函数与x轴的交点坐标是______; (3)代数式
(4)若s、t是两个不相等的实数,当s≤x≤t时,二次函数y=ax2+bx+c(a≠0)有最小值0和最大值24,那么经过点(s+1,t+1)的反比例函数解析式是______. |
答案
(1)根据抛物线图象的对称性由表中的数据可以得出:
当x=6时,y的值是:24;
(2)∵二次函数与x轴的交点坐标就是y=0时所对应的x的值,由表中的数据可得:
二次函数与x轴的交点坐标是(0,0),(2,0);
(3)原式=-
+(a+b+c)(a-b+c),当y=0时,由根与系数的关系及表中的数据得:-b a
=0+2=2,b a
a+b+c是x=1时y的值由表中数据得y=-1,∴a+b+c=-1,
a-b+c是x=-1时y的值由表中的数据得y=3,∴a-b+c=3,
∴原式=2+(-1)×3=2-3=-1;
(4)∵s、t是两个不相等的实数,s≤x≤t,
∴s<t.
∵当s≤x≤t时,二次函数y=ax2+bx+c(a≠0)有最小值0和最大值24,
∴由表中的数据可知y=0时,x=0或2,当y=24时,x=-4或6,
∴s=-4,t=0;s=-4,t=2;s=2,t=6
∴(s+1=-3,t+1=1);(s+1=-3,t+1=3);(s+1=3,t+1=7)
∵s=-4,t=2时y的最小值为-1.抛物线经过(-3,1),抛物线的顶点坐标是(1,-1),
∴最小值为-1,(舍去)
∴经过点(s+1,t+1)的反比例函数解析式是y=-
或y=3 x
.21 x
故答案为:24,(0,0),(2,0),-1,y=-
或y=3 x
.21 x

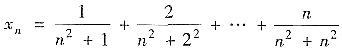 ,则
,则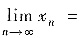 ______.
______.