问题
解答题
| 由多项式的乘法法则知：若（x+a）（x+b）=x2+x+q，则p=a+b，q=a·b；反过来x2+x+q=（x+a）（x+b）要将多项式x2+x+q进行分解，关键是找到两个数a、b，使a+b=p，a·b=q，如对多项式x2-3x+2，有p=-3，q=2，a=-1，b=-2。此时（-1）+（-2）=-3，（-1）（-2）=2，所以x2-3x+2可分解为（x-1）（x-2）即x2-3x-2=（x-1）（x-2）。 （1）根据以上填写下表： | ||||||||||||||||||||||||||||||
当q是正数时，应分解成两个因数a、b_______________号，a、b的符号与__________相同； 当q是负数时，应分解成的两个因数a、b______________号，a、b中绝对值较大的因数的符号与_______相同。 （3）分解因式： x2-x-12=_____________；x2-7x+6=________________。 |
答案
解：（1）9、20、4、5、
；-9、20、-4、-5、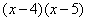
；1、-20、-4、5、
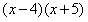；-1、-20、4、-5、
；
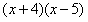（2）同、p，异、p；
（3）
。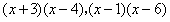