(1)证明：因为AD＝BC₀＝BD＝1，

AB＝C₀D＝，

所以∠DBC₀＝90°，∠ADB＝90°.

因为折叠过程中，∠DBC＝∠DBC₀＝90°，

所以DB⊥BC，又DB⊥BC₀，故DB⊥平面CBC₀.

又DB⊂平面ABC₀D，所以平面ABC₀D⊥平面CBC₀.

(2)法一：如右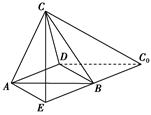图，延长C₀B到E，使BE＝C₀B，连结AE，CE.

因为AD綊BE，BE＝1，DB＝1，∠DBE＝90°，所以AEBD为正方形，AE＝1.

由于AE，DB都与平面CBC₀垂直，所以AE⊥CE，可知

AC＞1.

因此只有AC＝AB＝时，△ABC为等腰三角形．

在Rt△AEC中，CE＝＝1，又BC＝1，

所以△CEB为等边三角形，∠CBE＝60°.

由(1)可知，BD⊥BC，BD⊥BE，所以∠CBE为二面角A－BD－C的平面角，即二面角A－BD－C的大小为60°.

法二：以D为坐标原点，射线DA，DB分别为x轴正半轴和y轴正

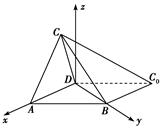
半轴，建立如右图的空间直角坐标系D－xyz，则

A(1,0,0)，B(0,1,0)，D(0,0,0)．

由(1)可设点C的坐标为(x,1，z)，其中z＞0，则有

x²＋z²＝1.①

因为△ABC为等腰三角形，所以AC＝1或AC＝.

若AC＝1，则有(x－1)²＋1＋z²＝1.

由此得x＝1，z＝0，不合题意．

若AC＝，则有(x－1)²＋1＋z²＝2.②

联立①和②得x＝，z＝.

故点C的坐标为.

由于DA⊥BD，BC⊥BD，所以与夹角的大小等于二面角A－BD－C的大小．

又＝(1,0,0)，＝，

cos〈，〉＝＝.

所以〈，〉＝60°，即二面角A－BD－C的大小为60°