问题
选择题
设函数f(x)的导函数为f′(x)，对任意x∈R都有f′(x)>f(x)成立，则( )
A．3f(ln 2)>2f(ln 3)
B．3f(ln 2)＝2f(ln 3)
C．3f(ln 2)<2f(ln 3)
D．3f(ln 2)与2f(ln 3)的大小不确定
答案
答案：C
构造函数g(x)＝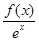
，则g′(x)＝
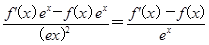>0，函数g(x)在R上单调递增，所以g(ln 2)<g(ln 3)，即
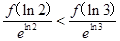，即3f(ln 2)<2f(ln 3)