问题
选择题
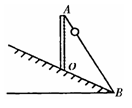
在离坡底10m的山坡上竖直地固定一长10m的直杆AO(即BO=AO=l0m),A端与坡底B间连有一钢绳,一穿心于钢绳上的小球从A点由静止开始沿钢绳无摩擦地滑下,如图所示,则小球在钢绳上滑行的时间为(取g=10m/s2)( )
A.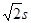
B.2 s
C.4s
D.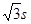
答案
答案:B
对小球受力分析,根据牛顿第二定律可以求得加速度的大小,再由匀变速直线运动的位移公式可以求得时间的大小.设∠OAB=α,对小球受力分析,
把重力分解为沿绳的mgcosα和垂直于绳的mgsinα,
小球受到的合力大小为mgcosα,
由牛顿第二定律得 mgcosα=ma,
所以下滑加速度为 a=gcosα,
AB长度 L=2?AOcosα=20cosα,
由位移公式可得:L=1/2at2
即 20cosα=1/2gcosα?t2
所以 t=2s.
故选B.
点评:由于不知道夹角的大小,不能求出加速度的具体的数值,但不妨碍求物体运动的时间的大小.
