解：基本事件总数的区域D的度量为正方形的面积，

即D的度量为S_正方形=6²=36，

由方程x²+2px-q²+1=0的两根都是实数得△=（2p）²-4（-q²+1）≥0，

所以p²+q²≥1，

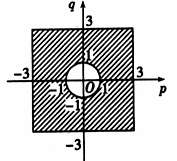
所以当点（p，q）落在如图所示的阴影部分时，

方程的两根均为实数，

由图可知，所求事件构成的区域D的度量为S_正方形-S_⊙O=36-π，

所以方程两根都是实数的概率为。