满足不等式组

-x+y-2≤0 x+y-4≤0 x-3y+3≤0

表示的平面区域如下图所示：

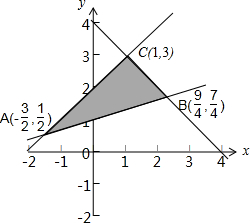
z=x²+y²表示可行域中动点（x，y）与原点距离的平方

故Z的最大值为OA²，OB²，OC²中的最大值

∵OA²=

5

2

，OB²=

65

8

，OC²=10

故当x=1．y=3时，z=x²+y²有最大值为10

Z的最小值为O点到直线x-3y+3=0的距离的平方

此时d²=

9

10

此时垂足为直线x-3y+3=0和3x+y=0的交点，解得x=-

3

10

，y=

9

10

故当x=-

3

10

，y=

9

10

时，z=x²+y²有最小值为

9

10