问题
选择题
已知函数f(x)=x2+2x+blnx,若函数f(x)在(0,1)上单调,则实数b的取值范围是
A.b≥ 0
B.b<-4
C.b≥0或b≤-4
D.b>0或b<-4
答案
C
题目分析:f'(x)=2x+2+ =
=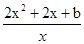 =
=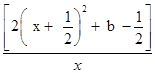 ,
,
∵g(x)="2x" ²+2x+b在(0,1)上单调,
∴当g(1)≤0,即4+b≤0,b≤-4时,f'(x)≤0,f(x) 在(0,1)上单调递减;
当g(0)≥0,即b≥0时,f'(x)≥0,f(x) 在(0,1)上单调递增,
综上,b≥0或b≤-4,选C。
点评:中档题,在给定区间,如果函数的导数非负,则函数为增函数,如果函数的导数非正,则函数为减函数。
