问题
解答题
抛物线y＝x2在点P处的切线与直线2x－y＋4＝0平行，求点P的坐标及切线方程．
答案
2x－y－1＝0
设点P(x0，y0)，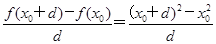
＝d＋2x0，
d→0时，d＋2xo→2x0.抛物线在点P处的切线的斜率为2x0，
由于切线平行于2x－y＋4＝0，∴2x0＝2，x0＝1
即P点坐标为(1,1)切线方程为y－1＝2(x－1)，即为2x－y－1＝0
搜题请搜索小程序“爱下问搜题”
抛物线y＝x2在点P处的切线与直线2x－y＋4＝0平行，求点P的坐标及切线方程．
2x－y－1＝0
设点P(x0，y0)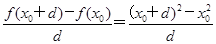，＝d＋2x0，
d→0时，d＋2xo→2x0.抛物线在点P处的切线的斜率为2x0，
由于切线平行于2x－y＋4＝0，∴2x0＝2，x0＝1
即P点坐标为(1,1)切线方程为y－1＝2(x－1)，即为2x－y－1＝0