问题
解答题
某分公司经销某种品牌的产品，每件产品的成本为3元，并且每件产品需向总公司交a（3≤a≤5）元的管理费，预计当每件产品的售价为x（9≤x≤11）元时，一年的销售量为（12-x）2万件。
（1）求分公司一年的利润L（万元）与每件产品的售价x的函数关系式；
（2）当每件产品的售价为多少元时，分公司一年的利润L最大，并求出L的最大值Q（a）。
答案
解：（1）分公司一年的利润L（万元）与售价x的函数关系式为：L=（x-3-a）（12-x）2，
x∈[9，11]。
（2）L′（x）=（12-x）2-2（x-3-a）（12-x）=（12-x）（18+2a-3x）
令L′（x）=0得x=6+
a或x=12（不合题意，舍去）
∵3≤a≤5，
∴8≤6+
a≤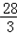
在x=6+
a两侧L′的值由正值变负值
所以，当8≤6+
a≤9，
即3≤a≤
时，Lmax=L（9）=（9-3-a）（12-9）2=9（6-a）；
当9＜6+
a≤
，即
＜a≤5时，Lmax=L（6+
a）=（6+
a-3-a）[12-（6+
a）]2=4（3-
a）3，
即当3≤a≤
时，当每件售价为9元，分公司一年的利润L最大，最大值Q（a）=9（6-a）万元；
当
＜a≤5时，当每件售价为（6+
a）元，分公司一年的利润L最大，最大值Q（a）=4（3-
a）3万元。