问题
解答题
函数f(x)=2x(ax2+bx+c)满足f(x+1)-f(x)=2x·x2(x∈R)，求常数a、b、c的值．
答案
解：由题设，ax2+(4a+b)x+2a+2b+c=x2，
由待定系数法，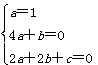
，
∴a=1，b=-4，c=6。
搜题请搜索小程序“爱下问搜题”
函数f(x)=2x(ax2+bx+c)满足f(x+1)-f(x)=2x·x2(x∈R)，求常数a、b、c的值．
解：由题设，ax2+(4a+b)x+2a+2b+c=x2，
由待定系数法，，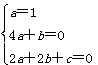
∴a=1，b=-4，c=6。