如图所示为某钢铁厂的钢锭传送装置,斜坡长为L=20 m,高为h=2 m,斜坡上紧排着一排滚筒.长为l=8 m、质量为m=1×103 kg的钢锭ab放在滚筒上,钢锭与滚筒间的动摩擦因数为μ=0.3,工作时由电动机带动所有滚筒顺时针匀速转动,使钢锭沿斜坡向上移动,滚筒边缘的线速度均为v=4 m/s.假设关闭电动机的瞬时所有滚筒立即停止转动,钢锭对滚筒的总压
力近似等于钢锭的重力.取当地的重力加速度g=10 m/s2.试求:

(1)钢锭从坡底(如上图示位置)由静止开始运动,直到b端到达坡顶所需的最短时间;
(2)钢锭从坡底(如上图示位置)由静止开始运动,直到b端到达坡顶的过程中电动机至少要工作多长时间?
(1)4 s (2)3.5 s
题目分析:(1)钢锭开始受到的滑动摩擦力为
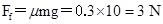
由牛顿第二定律有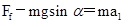
解得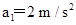
钢锭做匀加速运动的时间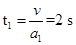
位移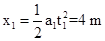
要使b端到达坡顶所需要的时间最短,需要电动机一直工作,钢锭先做匀加速直线运动,当它的速度等于滚筒边缘的线速度后,做匀速直线运动.
钢锭做匀速直线运动的位移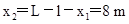
做匀速直线运动的时间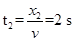
所需最短时间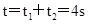 .
.
(2)要使电动机工作的时间最短,钢锭的最后一段运动要关闭电动机,钢锭匀减速上升,b端到达坡顶时速度刚好为零.
匀减速上升时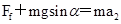
解得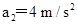
匀减速运动时间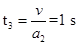
匀减速运动位移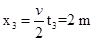
匀速运动的位移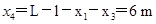
电动机至少要工作的时间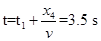 .
.
点评:本题关键是对木块受力分析,根据牛顿第二定律求出加速度,然后运用运动学公式列式求解.

