18

题目分析：由条件利用基本不等式可得xy=2x+y+6≥2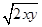+6，令xy=t²，即 t=＞0，可得t²-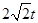t-6≥0．即得到(t-3)(t+)≥0可解得 t≤-，t≥3，又注意到t＞0，故解为 t≥3，所以xy≥18．故答案应为18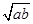解决最值问题的能力，以及换元思想和简单一元二次不等式的解法，属基础题

点评：解决该试题的关键是首先左边是xy的形式右边是2x+y和常数的和的形式，考虑把右边也转化成xy的形式，使形式统一．可以猜想到应用基本不等式a+b≥2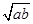．转化后变成关于xy的方程，可把xy看成整体换元后求最小值。