问题
选择题
函数f(x)=kx2-
|
答案
函数f(x)=kx2-
(k∈R)零点的个数,|x| x+4
即为函数y=kx2与y=
的图象交点个数,|x| x+4
在同一坐标系内分别作出函数y=kx2与y=
的图象,|x| x+4
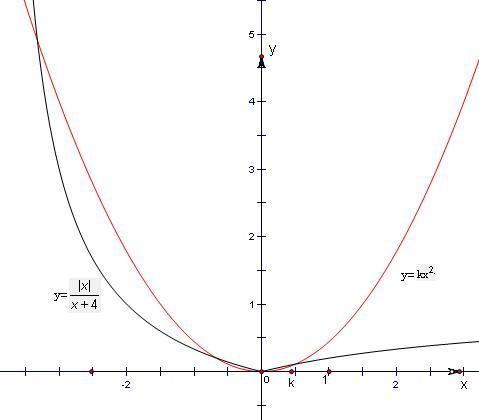
知两函数图象最多有4个交点,
即函数f(x)=kx2-
(k∈R)的零点个数最多是4.|x| x+4
故选D.
函数f(x)=kx2-
|
函数f(x)=kx2-
(k∈R)零点的个数,|x| x+4
即为函数y=kx2与y=
的图象交点个数,|x| x+4
在同一坐标系内分别作出函数y=kx2与y=
的图象,|x| x+4

知两函数图象最多有4个交点,
即函数f(x)=kx2-
(k∈R)的零点个数最多是4.|x| x+4
故选D.