问题
解答题
设A(x1，y1)，B(x2，y2)是平面直角坐标系xOy上的两点，现定义由点A到点B的一种折线距离ρ(A，B)为p(A，B)=|x2-x1|+|y2-y1|。对于平面xOy上给定的不同的两点A(x1，y1)，B(x2，y2)，
(Ⅰ)若点C(x，y)是平面xOy上的点，试证明ρ(A，C)+ρ(C，B)≥p(A，B)；
(Ⅱ)在平面xOy上是否存在点C(x，y)，同时满足
①ρ(A，C)+ρ(C，B)=ρ(A，B)；②ρ(A，C)=ρ(C，B)。
若存在，请求出所有符合条件的点；若不存在，请予以证明。
答案
(Ⅰ)证明：∵
，
，
∴
；
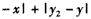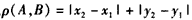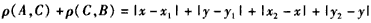
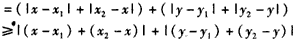
(Ⅱ)注意到点A(x1，y1)与点B(x2，y2)不同，下面分三种情形讨论．
(1)若x1=x2，则y1≠y2，
由条件②得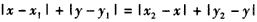
，
即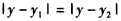
，∴
，
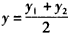由条件①得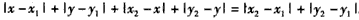
，
∴
，
∴
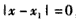，∴x=x1，
因此，所求的点C为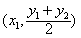
；
(2)若y1=y2，则x1≠x2，类似于(Ⅰ)，可得符合条件的点C为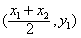
；
(3)当x1≠x2且y1≠y2时，不妨设x1＜x2，
(ⅰ)若y1＜y2，则由(Ⅰ)中的证明知，要使条件①成立，
当且仅当(x-x1)(x2-x)≥0与(y-y1)(y2-y)≥0同时成立，
故x1≤x≤x2且y1≤y≤y2，
从而由条件②，得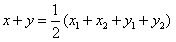
，
此时所求点C的全体为M={(x，y)|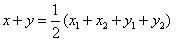
，x1≤x≤x2且y1≤y≤y2}；
(ⅱ)若y1＞y2，类似地由条件①可得x1≤x≤x2且y2≤y≤y1，
从而由条件②得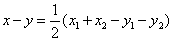
，
此时所求点的全体为{(x，y)|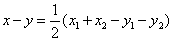，x1≤x≤x2且y2≤y≤y1}。
（）