问题
解答题
设平面向量am=(m,1),bn=(2,n),其中m,n∈{1,2,3,4},
(Ⅰ)请列出有序数组(m,n)的所有可能结果;
(Ⅱ)记“使得am⊥(am-bn)成立的(m,n)”为事件A,求事件A发生的概率。
答案
解:(Ⅰ)有序数组(m,n)的所有可能结果为:(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),共16个;
(Ⅱ)由am⊥(am-bn),得m2-2m+1-n=0,即n=(m-1)2,
由于m,n∈{1,2,3,4},
故事件A包含的基本事件为(2,1)和(3,4),共2个,
又基本事件的总数为16,
故所求的概率为P(A)=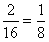 。
。
