问题
解答题
已知二次函数y=x2＋bx＋c与x轴交于A（－1，0）、B（1，0）两点.
（1）求这个二次函数的关系式；
（2）若有一半径为r的⊙P，且圆心P在抛物线上运动，当⊙P与两坐标轴都相切时，求半径r的值.
（3）半径为1的⊙P在抛物线上，当点P的纵坐标在什么范围内取值时，⊙P与y轴相离、相交？
答案
解：（1）由题意，得
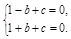解得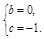
∴二次函数的关系式是y=x2－1．
（2）设点P坐标为（x，y），则当⊙P与两坐标轴都相切时，有y=±x．
由y=x，得x2－1=x，即x2－x－1=0，解得x=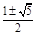
．
由y=－x，得x2－1=－x，即x2＋x－1=0，解得x=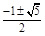
．
∴⊙P的半径为r=|x|=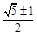
．
（3）设点P坐标为（x，y），∵⊙P的半径为1，
∴当y＝0时，x2－1=0，即x＝±1，即⊙P与y轴相切，
又当x＝0时，y＝－1，
∴当y＞0时， ⊙P与y相离；
当－1≤y＜0时， ⊙P与y相交.
（1）把A（-1，0）、B（1，0）代入y=x2+bx+c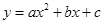
得到一个关于b、c的方程组，求出方程组的解即可得出二次函数的关系式；
（2）设点P坐标为（x，y），则当⊙P与两坐标轴都相切时，有y=±x，把y=±x分别代入由（1）求出的二次函数的关系式，求出x的值，即可得到半径r的值；
（3）设点P坐标为（x，y），先求出⊙P与y轴相切时x=±1，再根据圆与直线的位置关系的性质（r＜d时相离，r＞d相交）判断即可．