问题
问答题
设
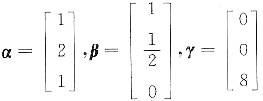，A=αβT，B=βTα，其中βT是β的转置．求解方程
2B2A2x=A4x+B4x+γ．
答案
参考答案：由题设，不难求得
[*]
而 A2=(αβT)(αβT)=α(βTα)βT=αβT=2A，
则A4=4A2=8A．由此可将原矩阵方程化简为16Ax=8Ax+16x+γ，即8(A-2E)x=γ，其中E为三阶单位矩阵．令x=(x1，x2，x3)T，代入上式，得
[*]
此方程组的增方矩阵为
[*]
经由初等行变换化为行简化阶梯形为
[*]
则导出组的基础解系为[*]而原方程组有特解[*]所以
[*]
其中C为任意常数．
解析：[考点提示] 矩阵方程．
