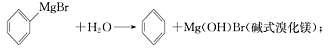已知二次函数y=-
(1)求出该函数图象的顶点坐标,对称轴,图象与x轴、y轴的交点坐标; (2)x在什么范围内时,y随x的增大而增大?当x在什么范围内时,y随x的增大而减小? (3)当x在什么范围内时,y>0? |
(1)y=-
(x2-2x)+2═-2 3
(x2-2x+1)+2+2 3
=-2 3
(x-1)2+2 3
,8 3
对称轴是x=1,
顶点坐标是(1,
),8 3
当y=0时:-
x2+2 3
x+2=0,4 3
解得:x1=-1,x2=3,
∴与x轴的交点坐标是:(-1,0)(3,0),
当x=0时:y=2,
∴与y轴的交点坐标是:(0,2);
(2)画图象可知:当x<1时,y随x的增大而增大,
当x>1时,y随x的增大而减小;
(3)由图象可知:当-1<x<3时,y>0.
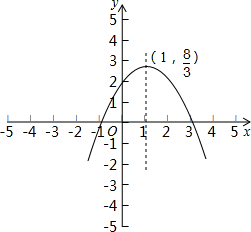

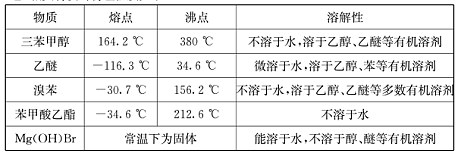
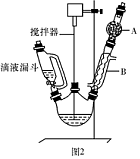
 )是一种重要的化工原料和医药中间体,实验室合成三苯甲醇的流程如图1所示,装置如图所示。
)是一种重要的化工原料和医药中间体,实验室合成三苯甲醇的流程如图1所示,装置如图所示。