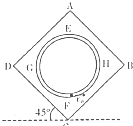
如图所示,在一匀强电场中,竖直面内有一正方形ABCD,CD边与水平面所成的角度为45°,CD边长为l=1m,电势φD=11V,φA=6V,φB=1V,ABCD内固定一个半径R=0.2m的光滑绝缘圆管,圆管的最上端、最下端=最左端和最右端分别为E、F、G、H,在圆管的底部有一质量m=1×10-6kg,电荷量为q=-×1C的小球从F点以v0=2m/s的速度在圆管内做完整的圆周运动小球的半径忽略不计,在运动过程中小球带电量不变.取g=10m/s2,以下说法正确的是( )
A.电场强度E=10V/m
B.小球在E点的速度为2m/s,且为圆周运动中的最小速度
C.小球在管中HE的中点时速度最小,且此时管壁对小球的作用力为零
D.以上说法都不对
A、因为DB中点电势为6V,与A点电势相等,所以电场方向水平向右,E==5V/m,故A错误.
B、小球所受的电场力大小F=qE=10-5N,重力大小G=mg=10-5N,则qE=mg,所以等效重力场沿BC方向,E点速度不是最小,轨迹EH的中点速度最小;故B错误.
C、D根据动能定理可算出EH中点的速度:-mg(R+R)-qER=m-m,=4(2-),当管壁没有作用力时的速度为v,mg=m,v2=gR=2m/s,因为<v2,所以里面的管壁对小球有作用力,故C错误,D正确.
故选D