问题
解答题
如图,B地在A地的正东方向,两地相距28km,A,B两地之间有一条东北走向的高速公路,A,B两地分别到这条高速公路的距离相等.上午8:00测得一辆在高速公路上行驶的汽车位于A地的正南方向P处.至上午8:20,B地发现该车在它的西北方向Q处,该段高速公路限速为110km/h,问该车有否超速行驶?
答案
作AO⊥PC于O点,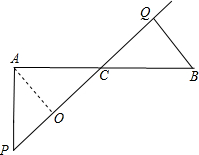
∵B在A正东方向,PQ为东北方向,
∴∠ACP=∠QCB=45°,
在Rt△ACO和Rt△BCQ中
∵
,∠AOC=∠BQC ∠ACO=∠QCB AO=BQ
∴△ACO≌△BCQ(角角边定理)
∴AC=BC=14,
由勾股定理得:OC=CQ=7
,2
∵P在A正南方向,
∴∠PAC=90°,
∴由勾股定理得:PC=√
AC=142
,2
所以PQ=PC+CQ=14
+72
=212 2
所以该车时速:21
÷2
=6320 60
<110,没超速,速度为632
km/h.2
