对某校高一年级学生参加社区服务次数进行统计,随机抽取了M名学生作为样本,得到这M名学生参加社区服务的次数,根据数据作出了频数的统计如下:
(Ⅱ)在所取样本中,从参加社区服务次数不少于20次的学生中任选2人,求至少有1人参加社区服务次数在区间[25,30)内的概率. |
(Ⅰ)20,0.2,4,0.25;(Ⅱ)
题目分析:(Ⅰ)因为在[10,15)小组中的频数为9,频率为0.45.则可算出样本数即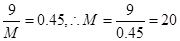 .所以m=20-9-5-2=4.又因为
.所以m=20-9-5-2=4.又因为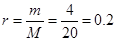 .所以可以求得结论.
.所以可以求得结论.
(Ⅱ)因为在所取样本中,从参加社区服务次数不少于20次的学生共有两组[20,25),[25,30).两组共有6人.通过列举在6人中任意选2人共有15种情况.所以其中没有一人在[25,30)组中的情况由6种.所以至少一人在[25,30)组中共有9种.所以可求出概率为 .
.
试题解析:(1)因为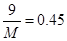 ,所以
,所以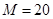 2分
2分
又因为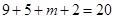 ,所以
,所以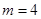 3分
3分
所以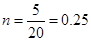 ,
,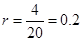 4分
4分
(2)设参加社区服务的次数在 内的学生为
内的学生为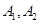 ,参加社区服务的次数在
,参加社区服务的次数在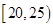 内的学生为
内的学生为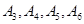 ; 5分
; 5分
任选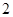 名学生的结果为:
名学生的结果为: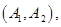
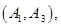
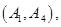
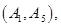
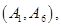

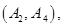
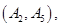
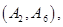
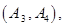
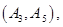
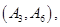
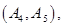
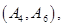
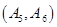 共
共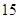 种情况 ; 8分
种情况 ; 8分
其中至少一人参加社区服务次数在区间 内的情况有
内的情况有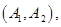
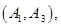
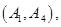
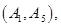
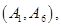

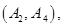
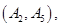
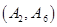 ,共
,共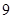 种情况
种情况
10分
每种情况都是等可能出现的,所以其中至少一人参加社区服务次数在区间 内的概率为
内的概率为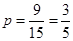 . 12分
. 12分
