问题
解答题
| 某班级举行一次知识竞赛活动,活动分为初赛和决赛两个阶段、现将初赛答卷成绩(得分均为整数,满分为100分)进行统计,制成如下频率分布表. | ||||||||||||||||||
(Ⅱ)决赛规则如下:参加决赛的每位同学依次口答4道小题,答对2道题就终止答题,并获得一等奖,如果前三道题都答错,就不再答第四题,某同学进入决赛,每道题答对的概率P的值恰好与频率分布表中不少于80分的频率的值相同, ①求该同学恰好答满4道题而获得一等奖的概率; ②记该同学决赛中答题个数为X,求X的分布列及数学期望。 |
答案
解:(Ⅰ)①8;②0.44;③6;④0.12;
(Ⅱ)由(Ⅰ)得,p=0.4,
①该同学恰好答满4道题而获得一等奖,即前3道题中刚好答对l 道,第4道也能够答对才获得一等奖,
则有 ,
,
②答对两道题就终止答题,并获得一等奖,所以,该同学答题个数为2,3,4,
即X=2,3,4,
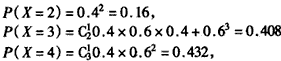
分布列为
X | 2 | 3 | 4 |
P | 0.16 | 0.408 | 0.432 |
