如图所示，水平轨道AB与放置在竖直平面内的1/4圆弧轨道BC相连，圆弧轨道的B端的切线沿水平方向．一质量m=1.0kg的滑块（可视为质点），在水平恒力F=5.0N的作用下，从A点由静止开始运动，已知A、B之间的距离s=5.5m，滑块与水平轨道间的动摩擦因数μ=0.10，圆弧轨道的半径R=0.30m，取g=10m/s2．
（1）求当滑块运动的位移为2.0m时的速度大小；
（2）当滑块运动的位移为2.0m 时撤去F，求滑块通过B点时对圆弧轨道的压力大小；
（3）滑块运动的位移为2.0m时撤去F后，若滑块恰好能上升到圆弧轨道的最高点，求在圆弧轨道上滑块克服摩擦力所做的功．
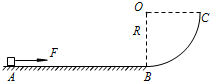
（1）设滑块的加速度为a1，根据牛顿第二定律
F-μmg=ma1
解得：a1=4.0m/s2
设滑块运动的位移为2.0m时的速度大小为v，根据运动学公式
v2=2a1s1
解得：v=4.0m/s
（2）设撤去拉力F后的加速度为a2，根据牛顿第二定律
μmg=ma2
解得：a2=μg=1.0m/s2
设滑块通过B点时的速度大小为vB，根据运动学公式
-v2=-2a2(S-S1)v 2B
解得：vB=3.0m/s
设滑块在B点受到的支持力为NB，根据牛顿第二定律
NB-mg=mv 2B R
解得：NB=40N
根据牛顿第三定律，滑块通过B点时对圆弧轨道的压力为40N．
（3）设圆弧轨道的摩擦力对滑块做功为W，根据动能定理
-mgR+W=0-
m1 2 v 2B
解得：W=-1.5J
圆弧轨道上滑块克服摩擦力所做的功为1.5J．
答：（1）求当滑块运动的位移为2.0m时的速度大小为4.0m/s；
（2）当滑块运动的位移为2.0m 时撤去F，滑块通过B点时对圆弧轨道的压力大小为40N；
（3）滑块运动的位移为2.0m时撤去F后，若滑块恰好能上升到圆弧轨道的最高点，在圆弧轨道上滑块克服摩擦力所做的功为1.5J．
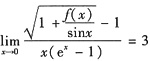．且当x→0时，f(x)与cxk是等价的无穷小，则常数c=______，k=______．