问题
填空题
若f(x)＝lg x，g(x)＝f(|x|)，则g(lg x)>g(1)，x的取值范围是________．
答案
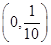∪(10，＋∞)
因为g(lg x)>g(1)，所以f(|lg x|)>f(1)，由f(x)为增函数得|lg x|>1，从而lg x>1或lg x<－1.解得0<x<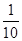
或x>10.
搜题请搜索小程序“爱下问搜题”
若f(x)＝lg x，g(x)＝f(|x|)，则g(lg x)>g(1)，x的取值范围是________．
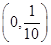∪(10，＋∞)
因为g(lg x)>g(1)，所以f(|lg x|)>f(1)，由f(x)为增函数得|lg x|>1，从而lg x>1或lg x<－1.解得0<x<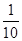或x>10.
