（1）∵f（x）=3^x，且f（a+2）=18，

∴3^a+2=18⇒3^a=2（2分）

∵g（x）=3^ax-4^x=（3^a）^x-4^x

∴g（x）=2^x-4^x（2分）

（2）g（x）在[0，1]上单调递减．证明如下

设0≤x₁＜x₂≤1

g(x2)-g(x1)=2x2-4x2-2x1+4x1

=(2x2-2x1)(1-2x1-2x2)（2分）

∵0≤x₁＜x₂≤1，

∴2x2＞2x1，1≤2x1＜2，1＜2x2≤2

∴2≤2x1+2x2＜4

∴-3＜1-2x1-2x2＜-1，

∴(2x2-2x1)(1-2x1-2x2)＜0

∴g（x₂）＜g（x₁）

∴g（x）在[0，1]上单调递减（2分）

（3）方程为2x -4x -b=0，

令t=2x x∈[-2，2]，则

1

4

≤t≤4（2分）

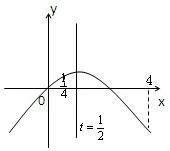
转化为方程为t-t²-b=0在[

1

4

，4]有两个不同的解．

∴b=t-t²即b=-(t-

1

2

)2+

1

4

，

当t=

1

2

时b取最大值

1

4

当t=

1

4

时，b=

3

16

，当t=4时，b=-12

可得，当

3

16

≤b＜

1

4

时，方程有两不同解．（4分）