问题
填空题
为了解甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14件和5件,测量产品中微量元素x,y的含量(单位:毫克).下表是乙厂的5件产品的测量数据:
(2)当产品中的微量元素x,y满足≥175且y≥75,该产品为优等品,用上述样本数据估计乙厂生产的优等品的数量; (3)从乙厂抽出的上述5件产品中,随即抽取2件,求抽取的2件产品中优等品数X的分布列及其均值(即数学期望). |
答案
(1)35件 (2)14(件)优等品 (3)X的分布列为
| X | 0 | 1 | 2 |
| P | 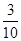 | 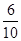 | 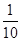 |
解:(1)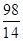 =7,5×7=35,即乙厂生产的产品数量为35件.
=7,5×7=35,即乙厂生产的产品数量为35件.
(2)易见只有编号为2,5的产品为优等品,所以乙厂生产的产品中的优等品,故乙厂生产有大约35×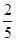 =14(件)优等品,
=14(件)优等品,
(3)X的取值为0,1,2.
P(X=0)=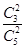 =
=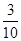 ,
,
P(X=1)=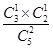 =
=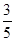 ,
,
P(X=2)=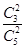 =
=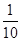 .
.
所以X的分布列为
| X | 0 | 1 | 2 |
| P | 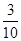 | 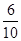 | 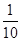 |
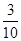 +1×
+1×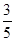 +2×
+2×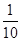 =
=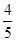 .
. 