问题
问答题
设矩阵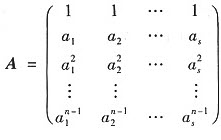
，其中ai≠aj(i≠j；i，j=1，2，…，s). 若B=ATA为正定矩阵，求s的值.
答案
参考答案：
(1)若s＞n. 注意到A的列向量组是s个n维向量. 必线性相关. 即存在X=(x1，s2，…，xs)T≠0，使AX=x1α1+x2α2+…+xsαs=0.
于是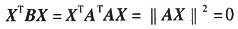
，与B为正定矩阵矛盾.
(2)若s=n，则A为n阶矩阵且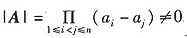
. 故A为可逆矩阵. 由B=ATA=ATEA知B与单位矩阵合同，从而B为正定矩阵.
(3)若s＜n，则A的前s行组成s个s维列向量，由范得蒙行列式不为0知其线性无关. 从而A的列向量组作为其延伸向量组仍线性无关. 对任意非零向量X=(x1，x2，…，xs)≠0，有AX=x1α1+x2α2+…+xsαs≠0.
从而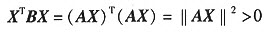
，即B亦为正定矩阵.
因此，B为正定矩阵的充分必要条件是s≤n.
解析：
[考点] 矩阵的正定性