问题
填空题
微分方程y"+4y=2x2在原点处与y=x相切的特解是______．
答案
参考答案：
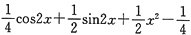
解析： 先求出特征根，再设出特解形式，代入原方程求之．
原方程所对应齐次方程的特征方程为
r2+4=0，解得r1,2=+2i．
故齐次方程通解为
Y1=c1cos2x+c2sin2x
设y*=ax2+bx+c是原方程的一个特解，代入原方程，比较两边系数可得
a=
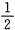，b=0，c=-
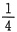，y*=
．
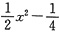故原方程的通解为
y=Y+y*=c1cos2x+c2sin2x+
．
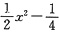由初始条件y|x=0=0，y’|x=0=1，可得c1=
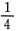，c2=
．
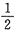y=
．
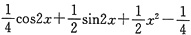