参考答案：

联系f(x)与f^’(x)的是拉格朗日中值定理，取x₀∈(a，+∞)，

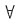x＞x0有f(x)=f(x₀)+f^’(ξ)(x-x₀)(x₀＜ξ＜x) ①因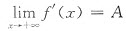，若A＞0，由极限的不等式性质可得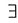，X＞a，当x＞X时，f^’(x)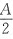＞．现取定x₀＞x，当x＞x₀时，由于ξ＞x₀＞x，有f^’(ξ)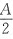＞，于是由①得f(x)＞f(x₀)+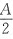(x-x₀)(x＞x₀)又因为

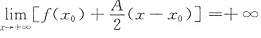，所以．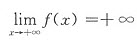

若A＜0，考察h(x)=-f(x)，则h^’(x)=-f^’(x)，

从而，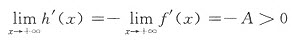

由已证结论知，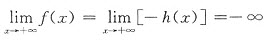

于是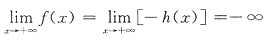．