问题
单项选择题
下 * * 个命题
①设
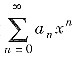的收敛域为(-R，R)，则
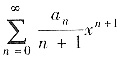的收敛域为(-R，R)；
②设幂级数
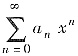在x=-1条件收敛，则它的收敛半径R=1；
③设幂级数
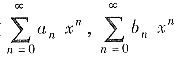的收敛半径分别为R1，R2，则
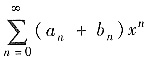的收敛半径R=min(R1，R2)
中正确的个数是
A．0个.
B．1个.
C．2个.
D．3个.
答案
参考答案：B
解析：此类选择题必须逐一判断，
关于命题①：对幂级数
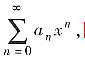逐项积分保持收敛区间不变，但收敛域可能起变化，如
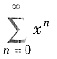的收敛域为(-1，1)，但
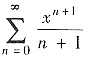的收敛域是[-1，1).
关于命题②：若熟悉幂级数的收敛性特点立即可知该命题正确.
记该幂级数的收敛半径为R. 若R＞1，由于
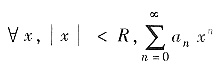绝对收敛
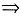
绝对收敛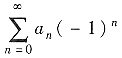，与已知矛盾，若R＜1，由
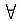x，|x|＞R，
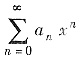发散
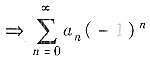发散，也与已知矛盾，因此，R=1.
关于命题③：当R1≠R2时，R=min(R1，R2)，于是要考察R1=R2的情形.
设有级数
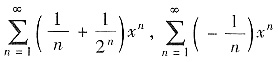，易求得它们的收敛半径均为R1=R2=1. 但
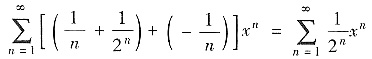的收敛半径为R=2. 因此命题不正确.
综上所述，应选B.
由
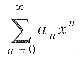在x=x0条件收敛
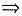该幂级数的收敛半R=|x0|，但不能确定
的敛散性.